НИР:Планирование задач в системах реального времени — различия между версиями
Материал из Кафедра Автоматики и телемеханики
Mvk (обсуждение | вклад) |
Mvk (обсуждение | вклад) |
||
| Строка 51: | Строка 51: | ||
В общем случае ''проблема планирования'' совокупности [[НИР:Периодические задачи РВ|периодических]] задач [[НИР:Жесткое реальное время|жесткого реального времени]] в случае [[НИР:Планирование с фиксированными приоритетами|концепции ПФП]] сводится к выбору такой совокупности {{nobr|<math>~\{O_i,\,T_i,\,\pi_i|i\in\left[1,n\right]{}\}</math>,}} которая обеспечивает соблюдение ограничений реального времени для ''всех'' <math>~n</math> задач. | В общем случае ''проблема планирования'' совокупности [[НИР:Периодические задачи РВ|периодических]] задач [[НИР:Жесткое реальное время|жесткого реального времени]] в случае [[НИР:Планирование с фиксированными приоритетами|концепции ПФП]] сводится к выбору такой совокупности {{nobr|<math>~\{O_i,\,T_i,\,\pi_i|i\in\left[1,n\right]{}\}</math>,}} которая обеспечивает соблюдение ограничений реального времени для ''всех'' <math>~n</math> задач. | ||
| − | Возможность изменения <math>~O_i,\,T_i</math> в заданных диапазонах, а также наличие <math>~n!</math> вариантов назначения приоритетов для <math>~n</math> задач приводят к тому, что полный перебор вариантов | + | Возможность изменения <math>~O_i,\,T_i</math> в заданных диапазонах, а также наличие <math>~n!</math> вариантов назначения приоритетов для <math>~n</math> задач приводят к тому, что полный перебор вариантов может стать практически труднореализуемым. |
| + | Нетрудно показать, что указанная проблема планирования является [http://en.wikipedia.org/wiki/NP-hard NP-трудной] <ref>Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. – М.: Мир, 1982.</ref>. | ||
| − | Поэтому естественный подход к ее решению – это разработка эффективных эвристических алгоритмов, которые за приемлемое время с высокой вероятностью находят значения {{nobr|<math>~\{O_i,\,T_i,\,\pi_i|i\in\left[1,n\right]{}\}</math>,}} обеспечивающие подходящий вариант планирования. | + | Поэтому естественный подход к ее решению – это разработка эффективных эвристических алгоритмов, которые за приемлемое время с высокой вероятностью находят значения {{nobr|<math>~\{O_i,\,T_i,\,\pi_i|i\in\left[1,n\right]{}\}</math>,}} обеспечивающие подходящий вариант планирования. Необходимость разработки таких алгоритмов становится особенно актуальной в случае систем, в которых планирование должно выполняться в процессе функционирования, например, при наличии возможности динамического добавления новой задачи. |
В данном очень простом примере была рассмотрена проблема планирования для [[НИР:Планирование с фиксированными приоритетами|концепции ПФП]]. Но существуют другие концепции планирования задач реального времени, и для каждой из них характерны свои специфические особенности проблемы планирования. | В данном очень простом примере была рассмотрена проблема планирования для [[НИР:Планирование с фиксированными приоритетами|концепции ПФП]]. Но существуют другие концепции планирования задач реального времени, и для каждой из них характерны свои специфические особенности проблемы планирования. | ||
Версия 00:52, 4 марта 2012
В системах автоматизации и управления, к которым, в частности, относятся системы автоматизации и управления (САиУ), часто надо осуществлять планирование задач реального времени, что предполагает разделение процессорного времени между этими задачами при условии соблюдения ограничений реального времени.
Определение проблемы планирования задач в системах реального времени
С общих позиций, проблема планирования задач реального времени состоит в обеспечении такого выполнения этих задач, которое гарантирует соблюдение всех ограничений реального времени этих задач.
В монографии [1] приводится следующее определение проблемы планирования.
Система жесткого реального времени должна выполнять множество задач реального времени, соперничающих за ресурсы, так, чтобы все критичные (с точки зрения времени) задачи укладывались в отведенные им крайние сроки. Для выполнения каждой задачи требуются вычислительные ресурсы, ресурсы данных и прочие ресурсы, например, устройства ввода-вывода. Тогда проблема планирования - это проблема такого распределения указанных ресурсов, которое обеспечивает соблюдение всех требований реального времени. |
Немного более детализированное определение используется в монографии [2]. С небольшой переформулировкой и уточнением его можно воспроизвести здесь следующим образом.
Имеется множество из Ограничения предшествования между задачами могут быть заданы в виде направленного ациклического графа. С каждой задачей могут связаны ограничения реального времени. Тогда проблема планирования - это проблема обеспечения такого назначения (за счет распределения по временной шкале) процессоров из |
Указанные определения являются довольно общими. В более конкретных условиях формулировка проблемы планирования становится более детализированной и более удобной для решения. Поясним это на следующем простом примере.
Пример проблемы планирования задач реального времени
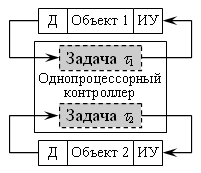
Пусть на однопроцессорном контроллере в составе САиУ выполняются две задачи реального времени, обозначаемые 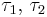 , для двух независимых контуров управления (см. рис. 1).
, для двух независимых контуров управления (см. рис. 1).
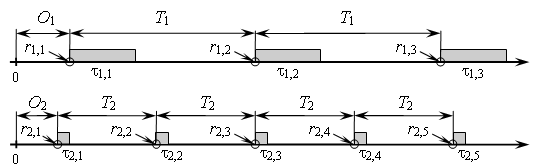
Каждая 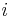 -я задача должна периодически формировать запросы
-я задача должна периодически формировать запросы 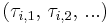 , и запросу требуется время выполнения (здесь для простоты оно считается постоянным) для формирования очередного воздействия на объект (см. рис. 2). В случае отдельного процессора для каждой задачи проблем не возникает, и они выполняются, как показано на рис. 2.
, и запросу требуется время выполнения (здесь для простоты оно считается постоянным) для формирования очередного воздействия на объект (см. рис. 2). В случае отдельного процессора для каждой задачи проблем не возникает, и они выполняются, как показано на рис. 2.
Однако при общем процессоре возникает взаимовлияние.
Пусть для разделения процессорного времени между задачами применяется концепция планирования с фиксированными приоритетами (ПФП).
Пусть начальные смещения 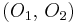 и периоды
и периоды 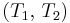 менять нельзя, тогда в рамках ПФП остается лишь менять приоритеты
менять нельзя, тогда в рамках ПФП остается лишь менять приоритеты 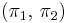 .
.
Поэтому существуют только два варианта планирования: 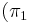 выше
выше 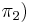 ,
, 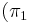 ниже
ниже 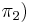 , приводящие к двум вариантам выполнения задач (см. рис. 3).
, приводящие к двум вариантам выполнения задач (см. рис. 3).
Согласно ПФП запрос задачи с более высоким приоритетом прерывает выполнение запроса задачи с более низким приоритетом. На рисунке окружностью отмечается момент 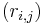 появления запроса
появления запроса 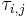 в очереди запросов, а прерывание запроса обозначается линией над соответствующей временной осью.
в очереди запросов, а прерывание запроса обозначается линией над соответствующей временной осью.
При этом 1-й вариант на рис. 3 приводит к значительному нарушению строгой периодичности для 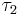 : видно, что
: видно, что 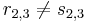 , где
, где 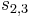 - начало выполнения
- начало выполнения 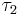 .
.
Простое изменение приоритетов приводит ко 2-му варианту на рис. 3, который обеспечивает строгую периодичность для 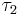 , и небольшое нарушение периодичности для
, и небольшое нарушение периодичности для 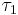 .
.
Пусть известно, что такое небольшое нарушение для 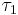 оказывается допустимым. Тогда решением проблемы планирования будет 2-й вариант на рис. 3 с соответствующими значениями
оказывается допустимым. Тогда решением проблемы планирования будет 2-й вариант на рис. 3 с соответствующими значениями 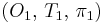 ,
, 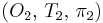 .
.
Однако в приведенном простом примере имеется всего два варианта планирования, и проблема планирования сводится к выбору одного из этих двух вариантов.
В общем случае проблема планирования совокупности периодических задач жесткого реального времени в случае концепции ПФП сводится к выбору такой совокупности 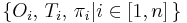 , которая обеспечивает соблюдение ограничений реального времени для всех
, которая обеспечивает соблюдение ограничений реального времени для всех 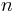 задач.
задач.
Возможность изменения 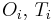 в заданных диапазонах, а также наличие
в заданных диапазонах, а также наличие 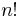 вариантов назначения приоритетов для
вариантов назначения приоритетов для 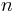 задач приводят к тому, что полный перебор вариантов может стать практически труднореализуемым.
Нетрудно показать, что указанная проблема планирования является NP-трудной [3].
задач приводят к тому, что полный перебор вариантов может стать практически труднореализуемым.
Нетрудно показать, что указанная проблема планирования является NP-трудной [3].
Поэтому естественный подход к ее решению – это разработка эффективных эвристических алгоритмов, которые за приемлемое время с высокой вероятностью находят значения 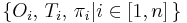 , обеспечивающие подходящий вариант планирования. Необходимость разработки таких алгоритмов становится особенно актуальной в случае систем, в которых планирование должно выполняться в процессе функционирования, например, при наличии возможности динамического добавления новой задачи.
, обеспечивающие подходящий вариант планирования. Необходимость разработки таких алгоритмов становится особенно актуальной в случае систем, в которых планирование должно выполняться в процессе функционирования, например, при наличии возможности динамического добавления новой задачи.
В данном очень простом примере была рассмотрена проблема планирования для концепции ПФП. Но существуют другие концепции планирования задач реального времени, и для каждой из них характерны свои специфические особенности проблемы планирования.
Примечания
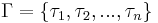 , множество из
, множество из 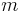 процессоров
процессоров 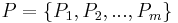 , а также множество из
, а также множество из 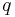 видов
видов 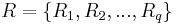 .
.
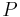 и ресурсов из
и ресурсов из 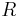 всем задачам из
всем задачам из 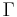 , которое обеспечивает завершение (или выполнение) всех задач согласно заданным ограничениям.
, которое обеспечивает завершение (или выполнение) всех задач согласно заданным ограничениям.