НИР:Планирование задач в системах реального времени — различия между версиями
Материал из Кафедра Автоматики и телемеханики
Mvk (обсуждение | вклад) |
Mvk (обсуждение | вклад) |
||
| Строка 3: | Строка 3: | ||
== Проблема планирования задач реального времени == | == Проблема планирования задач реального времени == | ||
| − | Поясним проблему планирования задач реального времени на следующем примере. | + | Поясним проблему планирования задач реального времени на следующем простом примере. |
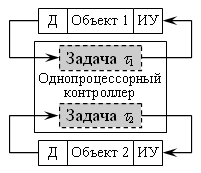
Пусть на однопроцессорном контроллере в составе САиУ выполняются две задачи реального времени, обозначаемые <math>\tau_1,\,\tau_2</math>, для двух независимых контуров управления (см. рис. 1). | Пусть на однопроцессорном контроллере в составе САиУ выполняются две задачи реального времени, обозначаемые <math>\tau_1,\,\tau_2</math>, для двух независимых контуров управления (см. рис. 1). | ||
| Строка 27: | Строка 27: | ||
Простое изменение приоритетов приводит ко 2-му варианту на рис. 3, который обеспечивает строгую периодичность для <math>~\tau_2</math>, и небольшое нарушение периодичности для <math>~\tau_1</math>. | Простое изменение приоритетов приводит ко 2-му варианту на рис. 3, который обеспечивает строгую периодичность для <math>~\tau_2</math>, и небольшое нарушение периодичности для <math>~\tau_1</math>. | ||
| + | |||
| + | Пусть известно, что такое небольшое нарушение для <math>~\tau_1</math> оказывается допустимым. Тогда решением проблемы планирования будет 2-й вариант на рис. 3 с соответствующими значениями <math>~(O_1,\,T_1,\,\pi_1)</math>, <math>~(O_2,\,T_2,\,\pi_2)</math>. | ||
| + | |||
| + | Однако в приведенном примере имеется всего два варианта планирования, и из них легко выбрать подходящий. Возможность изменения <math>~O_i,\,T_i</math> в заданных диапазонах, а также наличие <math>~n!</math> вариантов назначения приоритетов для <math>~n</math> задач приводят к тому, что полный перебор вариантов становится практически нереализуемым. Известно, что указанная проблема планирования является [http://en.wikipedia.org/wiki/NP-hard NP-трудной] <ref>Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. – М.: Мир, 1982.</ref>. | ||
| + | |||
| + | |||
{{-}} | {{-}} | ||
Версия 01:30, 26 декабря 2011
В системах автоматизации и управления (САиУ) для отдельного вычислительного устройства часто надо осуществлять планирование задач реального времени, что предполагает разделение процессорного времени между этими задачами при условии соблюдения ограничений реального времени.
Проблема планирования задач реального времени
Поясним проблему планирования задач реального времени на следующем простом примере.
Пусть на однопроцессорном контроллере в составе САиУ выполняются две задачи реального времени, обозначаемые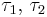 
, для двух независимых контуров управления (см. рис. 1).
(Д - датчик; ИУ - исполнительное устройство).
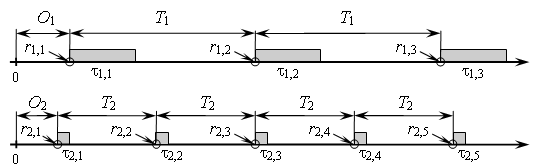
Каждая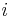 
-я задача должна периодически формировать запросы (
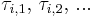), и запросу требуется время выполнения (здесь для простоты оно считается постоянным) для формирования очередного воздействия на объект (см. рис. 2). В случае отдельного процессора для каждой задачи проблем не возникает, и они выполняются, как показано на рис. 2.
в случае отдельных процессоров.Однако при общем процессоре возникает взаимовлияние.
Пусть для разделения процессорного времени между задачами применяется концепция планирования с фиксированными приоритетами (ПФП).
Пусть начальные смещения (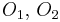
) и периоды (
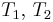) менять нельзя, тогда в рамках ПФП остается лишь менять приоритеты (
).
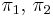Поэтому существуют только два варианта планирования: (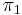
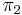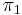выше 
), ( ниже 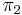), приводящие к двум вариантам выполнения задач (см. рис. 3).
в случае отдельных процессоров.Согласно ПФП запрос задачи с более высоким приоритетом прерывает выполнение запроса задачи с более низким приоритетом. На рисунке окружностью отмечается момент (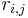
) появления запроса 
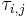в очереди запросов, а прерывание запроса обозначается линией над соответствующей временной осью.
При этом 1-й вариант на рис. 3 приводит к значительному нарушению строгой периодичности для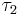 
: видно, что 
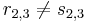, где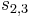 
- начало выполнения .
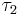Простое изменение приоритетов приводит ко 2-му варианту на рис. 3, который обеспечивает строгую периодичность для 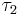, и небольшое нарушение периодичности для 
.
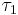Пусть известно, что такое небольшое нарушение для 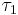оказывается допустимым. Тогда решением проблемы планирования будет 2-й вариант на рис. 3 с соответствующими значениями 
, 
.
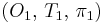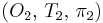Однако в приведенном примере имеется всего два варианта планирования, и из них легко выбрать подходящий. Возможность изменения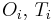 
в заданных диапазонах, а также наличие 
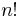вариантов назначения приоритетов для 
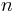задач приводят к тому, что полный перебор вариантов становится практически нереализуемым. Известно, что указанная проблема планирования является NP-трудной [1].
Примечания
- ↑ Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. – М.: Мир, 1982.
